Sparrow WebGL Devlog 8: Navigation Meshes and Pathfinding

Implementing navmeshes, A* pathfinding, and path smoothing in JavaScript and WebGL

09.07.2023 - 11:55
One of the hardest challenges in game development is pathfinding. Even in modern games like Age of Empires IV, you see a lot of people complaining about units taking weird routes or getting stuck. For an upcoming project, my Sparrow WebGL engine needs pathfinding, so I spend this week adding pathfinding and other related features.

Navigation Meshes

Before it's possible to calculate paths in a 3D environment, we need to start by defining and limiting that environment. The most general approach for 3D navigation is navigation meshes. Navigation meshes, also known as navmeshes, are used for efficient and realistic pathfinding for characters or entities in 3D worlds. A navigation mesh is a simplified representation of the game world, typically consisting of polygons or triangles that define walkable areas.

Other game engines like Unity or Unreal Engine are able to automatically bake a navmesh from a 3D environment. However, it's also possible to create the navmesh in Blender, export it, and import it as a normal mesh (see GLTF model loading). Once it's loaded, the mesh is converted into a navmesh by iterating over all triangles and adding all unique vertices as navmesh nodes. Then the triangle edges are used as connections for the nodes.

Normally, navmeshes are not rendered, but I added a debug renderer to make sure everything is loaded and converted correctly, so here is an example of how a navmesh would look like:



I have created the navmesh in a way where the nodes are at the vertices and the connections are along the triangle edges. However, there is also a different way of constructing the navmesh where the nodes are at the center of the triangles and connections go to all triangles with shared edges. I'm not sure whether one method is better than the other and there are probably some tradeoffs to either one depending on the exact situation.

Ray Casting

Last week, I implemented selecting objects in 3D space and I talked about why I chose color picking over ray casting. One of the reasons I mentioned was avoiding the math required for ray casting. Ironically, the first thing I had to implement this week was ray casting. While color picking is great for figuring out which object has been clicked, it does not return the position of the intersection. When clicking on a navmesh, however, you need to know the exact position of the intersection point in order to navigate to it.

Ray casting works by getting the position of the mouse in 2D screen space and then calculating the ray in 3D world space with the inverse view projection matrix. With the ray equation, it's possible to calculate the intersection between it and many different 3D shapes like boxes or spheres. The navmesh, however, is no neatly defined box, but an arbitrary triangle mesh instead. Therefore, we have to calculate the ray triangle intersection for all triangles of the navmesh. Luckily, I have implemented most ray casting features in my C++/OpenGL engine already, so it was mostly porting the code over to JavaScript and WebGL.

Pathfinding

With a navmesh representation and the ability to select exact positions on it, the actual pathfinding can begin. The most common pathfinding algorithm is A* (A star). It's versatile, relatively easy to understand, and finds the optimal path. I have implemented A* a few times already, including a JavaScript implementation for a Ludum Dare game, so it was easy to adapt to my WebGL engine.

Unlike a grid-based environment where the start and finish positions are neatly in a grid cell, a navmesh environment isn't quite as straightforward. When clicking on the navmesh, it's very unlikely that the click is close enough to a node for it to be used as the starting point. Instead, I'm adding temporary nodes to the navmesh for the start and finish that are connected to their closest neighbor. With this, A* can find the closest path on the navmesh from the start to the finish:

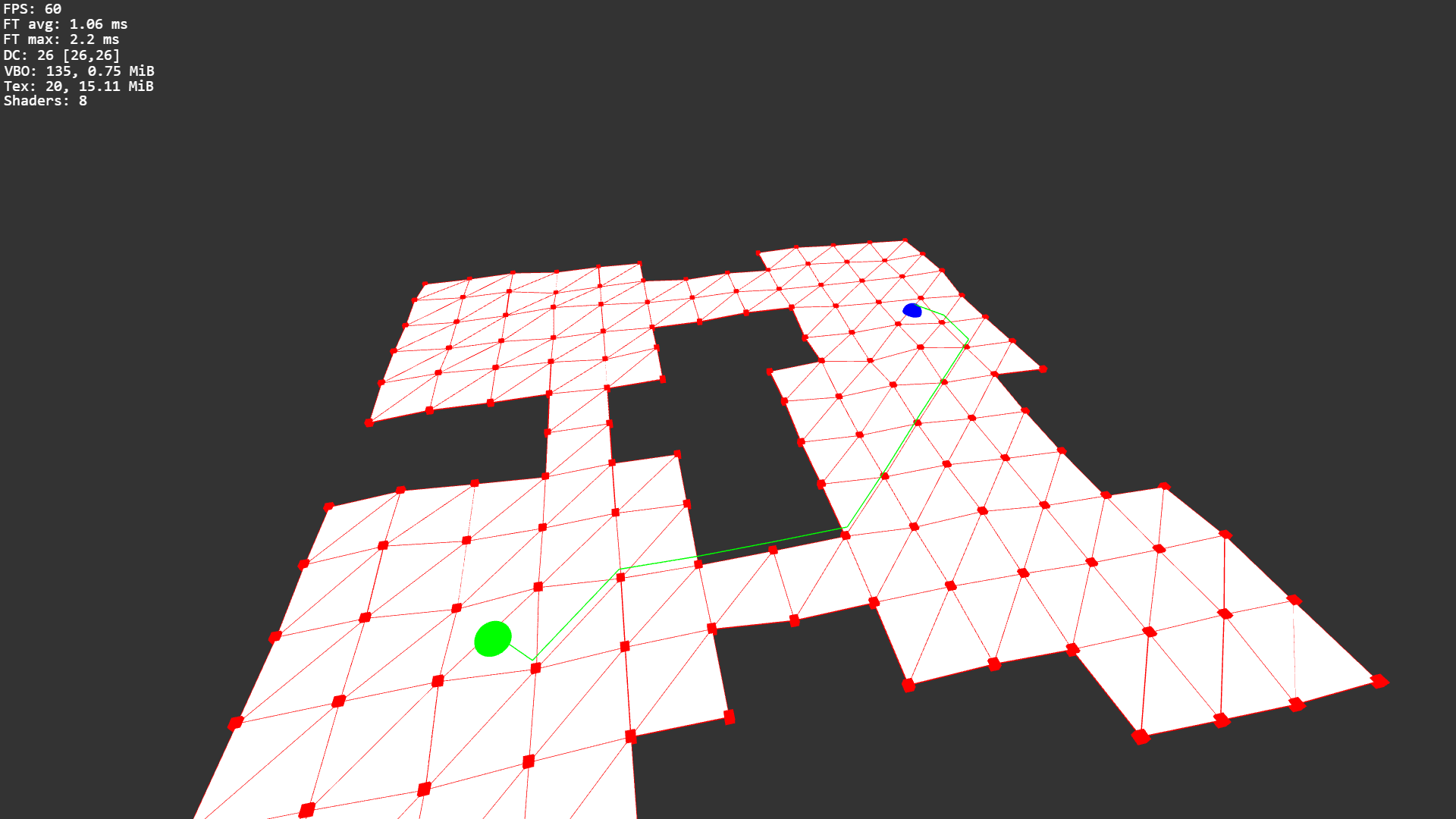
Path Smoothing

Now, when you look at the path in the image, you may notice that it's not really the shortest path. While A* is guaranteed to find the closest path between the nodes and connections of the navmesh, it isn't necessarily the shortest path in the 3D world because the navmesh is only a very rough approximation. Increasing the density of nodes and connections of the navmesh would improve the accuracy of the result. However, pathfinding on a very dense navmesh is quite slow, so a better solution is to keep the navmesh quite coarse and use a path smoothing algorithm on the result instead. Path smoothing is also known as string pulling because it's similar to pulling a string tight around obstacles.

The basic idea of path smoothing is to go through the path and check whether there is a direct line of sight between two nodes. If there is, the nodes in between can be removed and the path is updated to follow the direct line. I have implemented path smoothing for a previous project, but it was only used for that project and specific to its situation. The environment and navmesh were grid-based and there couldn't be any holes in the grid, so that solution isn't adaptable to a more general environment.

It's relatively easy to check for obstacles in the way when they have a hitbox, for example, a house, a tree, or a car by just calculating whether the line intersects with the box. However, the edges and potential holes in the navmesh are a much bigger problem. Theoretically, it would be possible to put hitboxes along the edges and over the holes, but you would need a lot of hitboxes to approximate any arbitrary navmesh shape. Not only would calculating the hitboxes themselves be difficult, but it would be slow to check such a large number of hitboxes.

After doing some research, I found the simple stupid funnel algorithm, but it works on navmeshes that are constructed with the nodes in the center of the triangles, and mine wasn't set up like that. Also, while the algorithm seems simple enough, it requires the corners to be arranged in a way that it's clear which ones are left and right relative to the path, which is a bit more complicated.

Rather than changing my navmesh setup, I experimented with a different solution for path smoothing. First of all, I'm only working with single-layer navmeshes, which means I can reduce the problem back down to two dimensions. When creating the navmesh, I render it once from a top-down perspective to a texture and then read the data from the texture to turn it into a black-and-white walkability mask.



To check whether two nodes have a direct walkable line between them, I take their delta vector and slowly step through it and sample the walkability mask. As soon as a point is obstructed, there is no direct line, and the function returns. The biggest problem with this approach is that the texture lookup coordinates are discrete, which means that when walking along an edge of the navmesh it's possible to be inside of the obstructed area of the mask because of rounding errors. However, when the non-smoothed path follows an edge of the navmesh, the path is already the shortest route and it doesn't have to be smoothed.

The most noticeable problem with my current solution is that it depends on the order of nodes in the original path. The algorithm starts from the beginning of the path and goes until it finds a node without a direct line and then skips all nodes between them. However, sometimes it would be better to go from node 1 to 3 and then to 6, instead of from 1 to 5 and then 6. I would have to try all combinations of nodes to find the truly shortest path which is a factorial problem that becomes extremely slow for longer paths. The current solution may not always return the shortest path, but it is convincing enough for most situations.

---

Pathfinding is a difficult challenge. While A* is simple enough, everything around it isn't as straightforward. Finding the perfect solution isn't always feasible, so you have to live with some approximations. My current implementation works for now, but I'm sure I'll have to make some changes when I want to use it for other projects in the future.

---